When it comes to Artificial Intelligence, Natural Language Processing is always discussed. It is one of the fundamental parts of AI and used in multiple applications. On a simple definition, Natural Language Processing is a group of computational techniques. These techniques are used to process and analyze data related to Natural Spoken or written languages.
Applications of Natural Language Processing:
- Classification of text
- spaCy Named Entity Recognition and providing them a Category. For example ‘Fruit to ‘Orange’.
- Creating a summary of large text data
- Sentiment Analysis
- Speech Recognition
- Checking Spelling and Grammar
- Recognition of Characters
- Creating Reports, Forecasts, Documentary from Analysis
- Checking Plagiarism in Text Documents
- Developing Automated Chatbots
These are some main applications of Natural Language Processing. It would take a whole another post for explaining all of the application domains. So as you all can see that NLP helps to deal with text data to carry out further analysis and create various AI applications.
Programming languages such as Python provides multiple libraries for performing NLP. Earlier NLTK – Natural Language Tool Kit was used to perform NLP operations in Python.
But in this post we will be discussing implementing spaCy Library, A new python open-source library specially developed for Natural Language Processing. So let us get started with Python spaCy Library:
What is spaCy?
spaCy is an open-source library for handling Advanced Natural Language Processing. It is written mainly in programming languages Python and Cython.
The previously used NLP library NLTK was mostly used for research purposes. spaCy library on the other hand works on providing software applications. This software could be used to build modules in further production.
spaCy also helps in connecting models developed and trained by other Machine Learning libraries. This support is provided to libraries such as TensorFlow, Scikit-Learn, and Keras. It does the work faster and the developer does not need to worry about algorithms being used.
General Features of spaCy Library
1. Fast and Accurate – Because of the data structure that it uses spaCy provides faster and better results.
2. Language Support – spaCy Library has support for more than 50 languages which makes it all in one tool for NLP.
3. Statistical Models – Spacy has 16 such models for 9 languages. It also allows connecting these models from other ML libraries.
4. spaCy Named Entity Recognition – The library allows you to perform Named Entry Recognition efficiently.
5. Tokenization – Spacy uses non-destructive segmentation of text into words and punctuation.
6. Deep Learning – It provides an easy to integrate process for Deep Learning algorithms.
7. Rule-Based Morphology – The root word is modified by adding prefixes and suffixes.
8. Part of Speech Tagging – The tokenization breaks the text into segments on which tags could be applied.
9. Visualization made Easy – spaCy has built-in support for Syntax and NER visualization.
10. Array Support – You can deploy or export the data modules into NumPy arrays directly.
These were a few of the linguistic features of the Spacy library. Now we will be looking at the implementation spaCy for Natural Language Processing.
Installing spaCy Library and Setting it Up
1. First, you will need to Download spaCy from here
2. Unzip the file that you have downloaded.
3. Use the following command for installing the spaCy package.
Python setup.py install
4. Installation Code for Linux Users
sudo pip install spacy sudo python -m spacy download en sudo python -m spacy download fr
5. Installation Code for Windows Users
pip install spacy
6. Installing through Anaconda Platform
conda install tqdm conda install spacy/conda install -c conda-forge spacy python -m spacy download en
Important Note: You can use both Pip or Pip3 for the Installation.
7. spaCy could be used for analyzing and processing many languages. For our work, we will be using the English language and it can be installed by the following code:
python -m spacy download en
It is already written in the Anaconda code above. If you are using any other development platform then go with the code on the individual.
Now we have installed the package in our machine. The next part is the spaCy implementation and looking at the features with Python.
Implementation of spaCy Library
1. Importing Spacy and Loading English Language
import spacy
nlp = spacy.load('en')
2. Reading a Text Document through Spacy
doc1=nlp("Hello, We Are Working on Spacy")
doc1
3. Reading a Text File
myfile = open("learnspacy.txt").read()
myfile
file1=nlp(myfile)
file1
Output Screen:
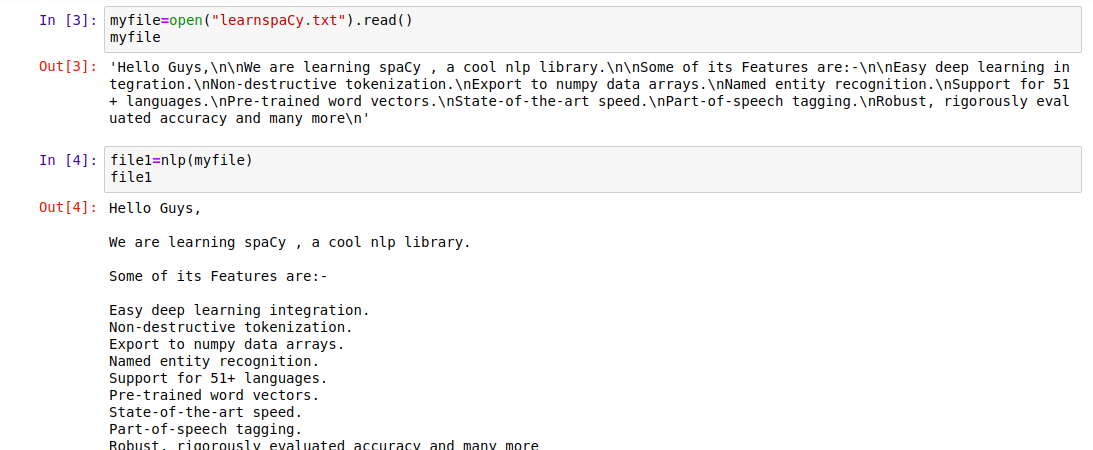 |
| Reading File with Spacy |
4. Sentence Tokenization with Spacy Library
for num, sentence in enumerate(file1.sents):
print(f'{num} : {sentence}')
Output Screen:
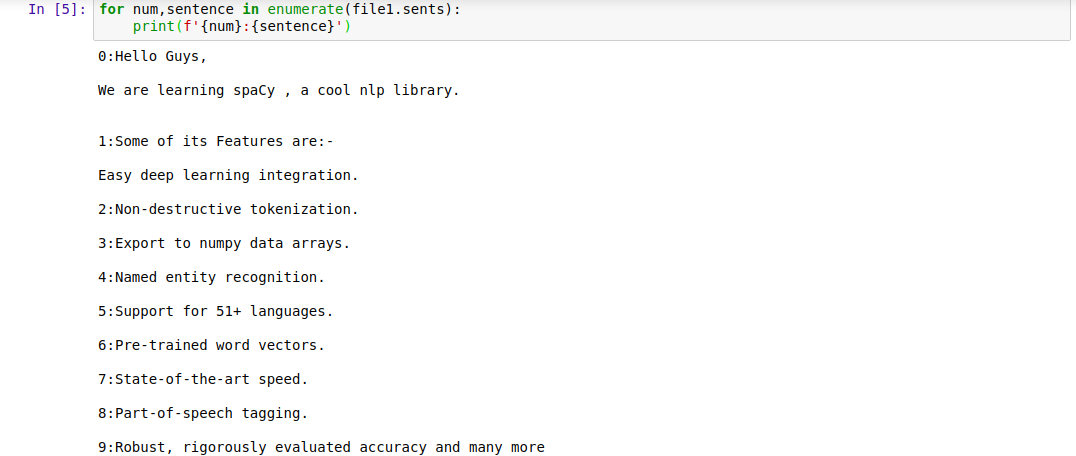 |
| Sentence Tokenization |
We can see that each segment is given an index number to be represented.
5. Word Tokenization
doc1
for token in doc1 :
print(token.text)
Output Screen:
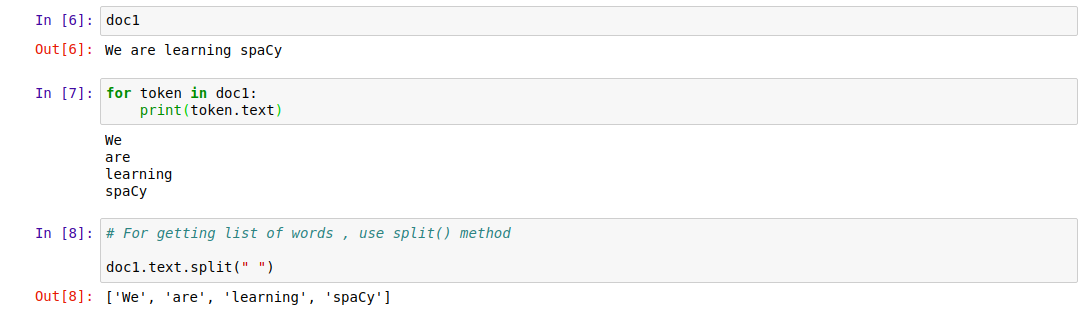 |
| Word Tokenization |
6. Some features related to Words
.is_alpha : Returns boolean True or False for if the word is an alphabet or not.
.is_stop : Returns boolean True or False for if the word is a stop word or not.
.shape : Tells about the shape of the word either if it is lowercase or uppercase.
The small x above represents a lowercase word and capital X represents an uppercase word.
Output Screen:
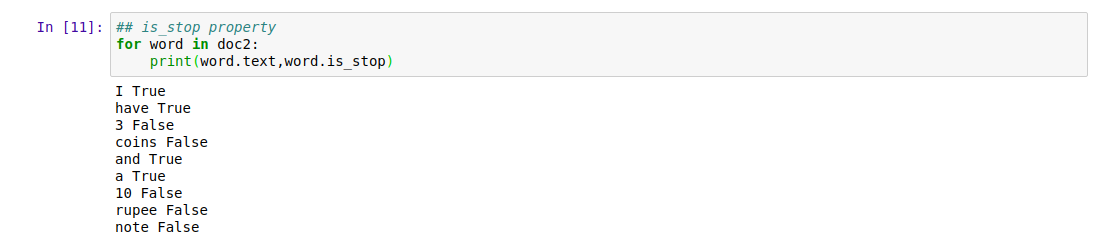 |
| Features Related to Word |
7. Parts of Speech Tagging
NP attribute_ : Returns a string representation of attribute
.pos_ : It is used for exposing Google universal pos_tag, simple.
With the help of this property part of speech corresponding to any word could be seen and analyzed.
.tag_ : Helps with the treebank for training a new model from scratch.
Tag may be used to represent pos abbreviation. Look at the image below for understanding pos abbreviations better.
Output Screen:
 |
| Meaning of Pos Abbreviations |
8. Visual Dependency using spaCy Displacy
Used to describe relations between individual tokens. Could be used with both subject and object token words.
Output Screen:
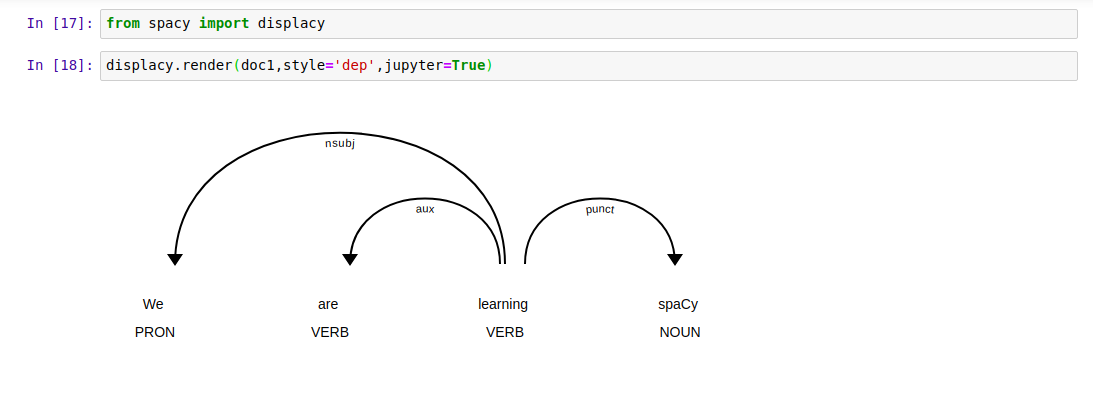 |
| Visual Dependency |
9. Lemmatization
Lemmatization is the technique to group together words with a kind of same meaning. This way we can move to the root of any word. All the search engines use lemmatization in filtering user queries.
The queries entered by users can be grouped and a base word could be identified to show perfect results. This enables the search engines to show results closely relevant to the user-submitted queries.
Output Screen:
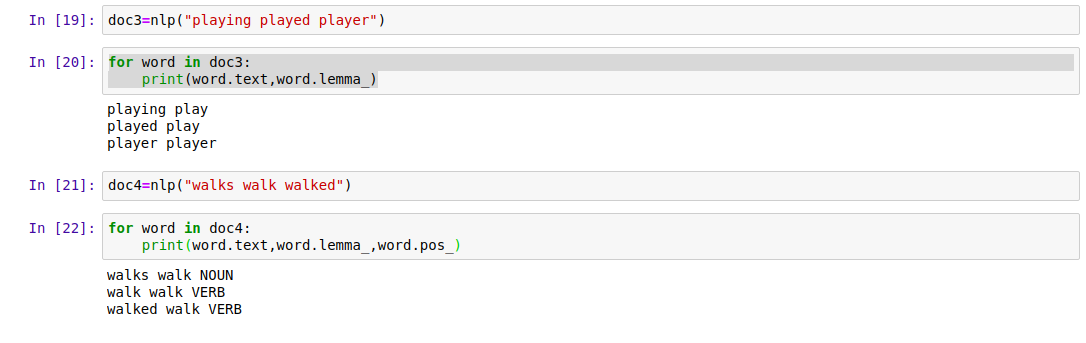 |
| Lemmatization with Spacy |
10. spaCy Named Entity Recognition
spaCy Named Entity Recognition is used to categorize words based on some classifications. The categories may be predefined or close to real-world entities. For example, whenever it scans the word Orange it will put it in the Fruit category after matching closely related words.
NER has various applications in Search Engines, Recommendation systems, Data Extractor tools, etc.
Output Screen:
 |
| spaCy Named Entity Recognition |
11. Semantic Similarity
This feature is very much helpful for Data Scientists to filter out tons of data. You can install it using the following command:
Code for performing Semantic Similarity check:
doc5=nlp("cat dog bird fish")
for w1 in doc5 :
for w2 in doc5 :
print((w1.text, w2.text), "Similarity :-",w1.similarity(w2))
You can find a similarity between two words or wither two sentences as shown in the images below.
Output Screen:
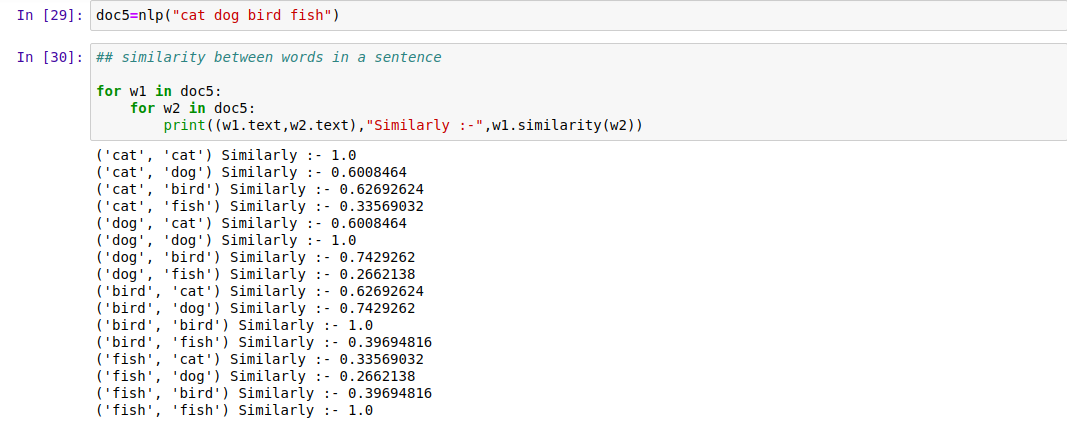 |
| Similarity Between Words |
12. Finding and Adding Stopwords
Stop words are the most common words used in any of the languages. They are mostly ignored by language processors and does not hold any value to the actual text and its content for the meaning part. For example Is, The, of, On, etc.
from spacy.lang.en.stop_words import STOP_WORDS
STOP_WORDS.add('ohh')
nlp.vocab["ohh"].is_stop
Output Screen:
 |
| Adding Stopwords to Vocab |
13. spaCy Noun Chunks
They are the base noun phrases and always have a head noun on them. For example a noun with a word that describes the noun.
Output Screen:
 |
| Noun Chunks |
Get the head of with spaCy noun chunk by the following code:
for w in doc1.noun_chunks:
print(w.root.text)
Find connectors between noun chunks by the code given below:
for w in doc1.noun_chunks:
print(w.root.text, "--connected by=", w.root.head.text)
14. Sentence Segmentation and Detection of Boundary
With the help of this feature, we can easily determine the end of any sentence. This is used for segmenting sentences for analysis. The end of the sentence could be found by these factors.
- The occurrence of a Period(.)
- If the next word starts with capital after a period.
- End line character (‘n’)
- Any other sentence breaker including ‘?’
Code for performing sentence segmentation and boundary detection:
doc2=nlp("Hello friends, we are learning spaCy tutorial. Are you all enjoying? keep learning")
for sent in doc2.sents:
print(sent)
Output Screen:
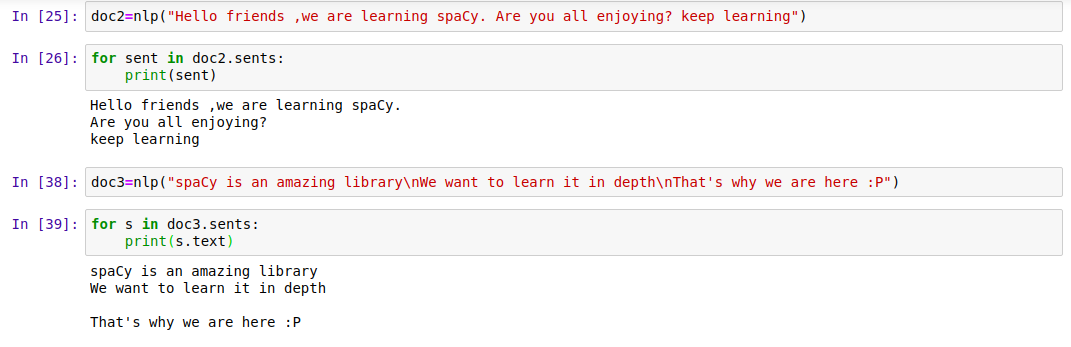 |
| Sentence Segmentation |
So this was all about the implementation of an Amazing Python and Machine Learning Library spaCy. We have tried to cover all the major implementations of the spaCy library for Natural Language Processing and included the codes wherever needed.
If you have got any doubts then you can check the Repository for complete code: Spacy GitHub
Hope you will like the article on the Spacy tutorial Machine Learning Library.

Too good��